前言

今天这个模型说实话有点绕，不是蛮好理解，但是其在自然语言处理、语音识别和模式识别等众多工业领域上都有着极为广泛的应用。因此隐马尔科夫模型也是面试中的必考算法之一！

唔使担心！今天和阿南一起搞定 隐马尔科夫模型。

隐马尔可夫模型

首先，我们要直到这东西有啥用，学来做什么！

隐马尔可夫应用目的： *通过可观测到的数据，计算、预测不可观测到的数据。*

接下来让阿南解释一下 隐马尔可夫模型 这个名字的由来！

隐马尔科夫模型 (Hidden Markov Model, HMM) ，用于描述由 隐藏的马尔可夫链 随机生成观测序列的过程。

因为包含每个时刻状态信息的马尔可夫链是隐藏的、不可观测的，因此称之为隐马尔可夫模型。

那啥子是 马尔可夫链 呢？

这里直接给出书上的定义：

马尔可夫链描述了一种状态序列，其每个状态值只取决于前面的有限个状态。 马尔可夫链是具有马尔可夫性质的随机变量的一个数列。这些变量的范围，即状态 $i$ 所有可能取值的集合 $Q$ 称之为状态空间 $Q = {q_1, q_2, …, q_N}$。

给出一张图片进行说明：

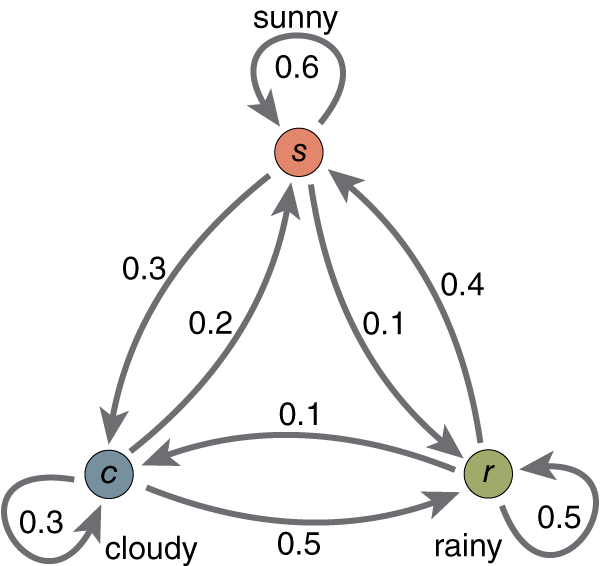
如上图所示，这里一共只有三个状态，分别是 晴天 (Sunny)，阴天 (Cloudy) 和 雨天 (Rainy)。其状态空间就是 $Q = {晴天，阴天，雨天 }$。

这里以晴天为例子，从图中我们可以得知当前时刻 $t$ 是晴天这个状态，那么：

• 下一时刻 $t+1$ 继续是晴天这个状态的概率是 $0.6$
• 下一时刻 $t+1$ 是阴天这个状态的概率是 $0.3$
• 下一时刻 $t+1$ 是雨天这个状态的概率是 $0.1$

并且，这三者的概率之和为 $1$。这个就是状态转移概率，稍后我们会详细介绍！

接下来再给出李航老师《统计学习方法》上关于隐马尔可夫模型的定义：

隐马尔可夫模型： 隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测从而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，成为状态序列 $I$；每个状态生成一个观测，而由此产生的观测的随机序列，成为观测序列 $O$。序列的每一个位置都可以看作是一个时刻。

接下来给出一张阿南辛辛苦苦画滴图！

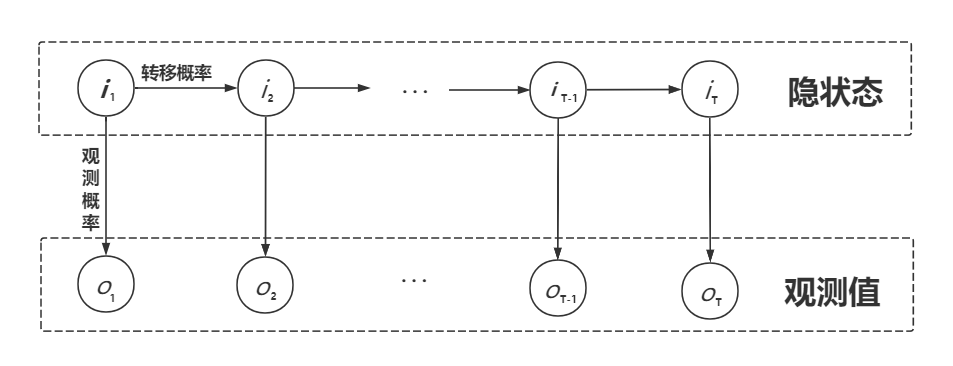
隐马尔可夫模型由 初始概率分布、状态转移概率分布 以及 观测概率分布 三者所确定。具体形式定义如下：

设 $Q$ 是所有可能的 $N$ 个状态的集合，$V$ 是所有可能的 $M$ 个观测的集合：

\[Q=\{q_1, q_2,...,q_N\},\qquad V=\{v_1, v_2,...,v_M\}\]

接着定义长度为 $T$ 的状态序列 $I$ 及其对应的观测序列 $O$：

\[I=(i_1, i_2,...,i_T),\qquad O=(o_1, o_2,...,o_T)\]

状态转移概率矩阵 $A$：

\[A = [a_{ij}]_{N\times N} \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1N} \\ a_{21} & a_{22} & \cdots & a_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ a_{N1} & a_{N2} & \cdots & a_{NN} \end{bmatrix} \tag{1}\]

其中，$a_{ij}$ 是时刻 $t$ 处于状态 $q_i$ 的条件下于下一时刻 $t+1$ 转移到状态 $q_j$ 的概率：

\[a_{ij} = P(i_{t+1}=q_j|i_t=q_j),\qquad i=1,2,...,N;\qquad j=1,2,...,N \tag{2}\]

观测概率矩阵 $B$：

\[B = [b_j(k)]_{N\times M}= \begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1M} \\ b_{21} & b_{22} & \cdots & b_{2M} \\ \vdots & \vdots & \ddots & \vdots \\ b_{N1} & b_{N2} & \cdots & b_{NM} \end{bmatrix} \tag{3}\]

其中 $b_j(k)$ 即第 $j$ 行，第 $k$ 列的值表示的是系统或过程在时刻 $t$ 在状态 $q_j$ 的条件下生成观测 $v_k$ 的概率：

\[b_j(k) = P(o_t = v_k | i_t = q_j), \qquad k=1,2,...,M;\qquad j=1,2,...,N \tag{4}\]

初始状态概率向量 $\pi$:

\[\pi = [\pi_1, \pi_2 ,...,\pi_N] \tag{5}\]

其中 $\pi_i$ 是时刻 $t=1$ 处于状态 $q_i$ 的概率。

隐马尔可夫模型由 初始状态概率向量 $\pi$、状态转移概率矩阵 $A$、观测概率矩阵 $B$ 三者决定。其中 $\pi, A$ 决定状态序列，$B$ 决定观测序列。 我们用三元符号来表示隐马尔可夫模型：

\[\lambda = (A, B, \pi) \tag{6}\]

其中状态转移概率矩阵 $A$ 与初始状态概率向量 $\pi$ 确定了隐藏的马尔可夫链并生成不可观测的状态序列 $I$。观测概率矩阵 $B$ 确定了如何从某个状态 $i$ 生成观测，与状态序列一起综合确定了如何产生观测序列 $O$。

并且，隐马尔可夫模型做出了三个基本假设：

1. 马尔可夫假设： 当前时刻的状态值，仅依赖于前一时刻的状态值，并不依赖于更早时刻的状态。

   \[P(i_t|i_{t-1}, o_{t-1},...,i_1, o_1) = P(i_t|i_{t-1}), \qquad t=1,2,...,T \tag{7}\]

2. 齐次马尔可夫性假设： 状态转移概率矩阵与时间无关。即所有时刻共享同一个状态转移矩阵。

3. 观测独立性假设： 任意时刻的观测仅依赖当前时刻马尔可夫链的状态，与其它观测及状态无关：

   \[P(o_t|i_T,o_T,i_{T-1}, o_{T-1},...,i_{t+1}, o_{t+1},i_t,o_t,i_{t-1}, o_{t-1},...,i_1, o_1) = P(o_t|i_t) \tag{8}\]

由于隐马尔可夫模型是对概率建模，通过数据学习联合概率分布 $P(O,I)$，进而求出条件概率分布 $P(I\mid O)$ 作为预测的模型，即 生成模型。

由于以上特性，隐马尔可夫模型可用于标注，此时状态 $i$ 对应着标记。标注问题指的是给定观测序列，预测其对应的标记序列 $I$。

三个基本问题

既然讲了这个模型，那这个 隐马尔可夫模型 有啥子用呢？阔以解决啥子问题呢？接下来就要讲讲它阔以解决的三个基本问题：

1. 概率计算问题： 给定模型 $\lambda=(A,B,\pi)$ 和观测序列 $O=(o_1, o_2, …,o_T)$，计算在模型 $\lambda$ 下观测序列 $O$ 出现的概率 $P(O\mid \lambda)$。

2. 学习问题： 在已知观测序列 $O=(o_1, o_2, …,o_T)$ 的情况下，用极大似然估计的方法估计模型 $\lambda = (A,B,\pi)$ 的参数，使得在估计得到的模型参数 $\lambda$ 下观测序列 $O=(o_1, o_2, …,o_T)$ 出现的概率 $P(O\mid \lambda)$ 出现的概率最大。

3. 预测问题： 在已知模型 $\lambda = (A,B,\pi)$ 和观测序列 $O=(o_1, o_2,…,o_T)$, 求对给定观测序列 $O$ 下最有可能的状态序列 $I=(i_1, i_2,…,i_T)$。即给定观测序列，求最有可能对应的状态序列。

首先我们先从第一个基本问题开始~

概率计算问题

观测序列概率 $P(O\mid \lambda)$ 的计算方法分为 前向算法 (forward) 和 后向算法 (backward)。

前向概率

前向概率的计算可以用李航老师的一张图来形象滴理解~

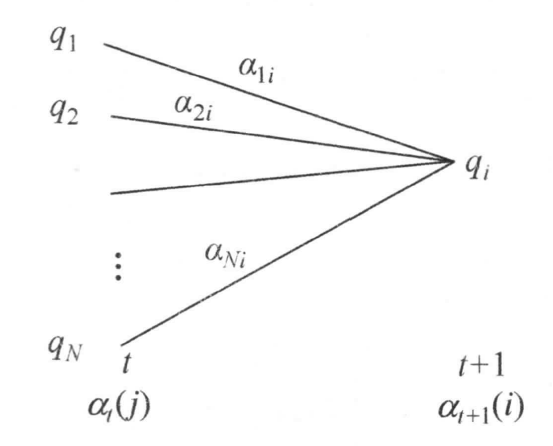
（来自《统计学习方法》199页）

首先给出 前向概率 的定义：

给定隐马尔可夫模型 $\lambda$，定义到时刻 $t$ 时部分观测序列为 $o_1, o_2, …, o_t$ 且在 $t$ 时刻的状态为 $i_t = q_i$ 的概率为前向概率，记作 $\alpha_t(i)$

\[\alpha_t(i) = P(o_1, o_2, ..., o_t, i_t=q_i|\lambda) \tag{9}\]

那么，我们应该怎么样根据前向概率 $\alpha_t(i)$ 去求得观测序列概率 $P(O\mid \lambda)$ 呢？答案就是 递归 (recursion)！

1. 计算前向概率的初值！（因为第一次嘛，总是有点特殊的！）

   \[\alpha_1(i) = \pi_i b_i(o_1),\qquad i=1,2,...,N \tag{10}\]

   这个也很好理解，初始时刻状态 $q_i$ 的前向概率 $\alpha_1(i)$ 就是当前状态 $q_i$ 发生的概率 $\pi_i$ 乘以在这个状态下产生第一个观测 $o_1$ 的概率 $b_i(o_1)$。

2. 递归地求 $t=1,2,…,T-1$ 个时刻下的前向概率

   \[\alpha_{t+1}(i) = \left[\sum_{j=1}^N \alpha_t(j) a_{ji} \right] b_i(o_{t+1}) \tag{11}\]

   这个叻，就有一点点绕，不过请紧跟阿南脚步！

   我们仔细观察可以发现，新时刻 $t+1$ 的前向概率根据定义就应该是在上一时刻的任务已经完成的情况下（也就是 $\alpha_{t}(j)$）我们要将状态从 $t$ 时刻的 $i_t = q_j$ 先转移至下一时刻，也就是 $t+1$ 时刻的状态 $i_{t+1}=q_i$，所以要乘上转移概率 $\alpha_{ji}$。然后在此基础上，我们再乘上新时刻在状态 $q_i$ 下产生产生观测 $o_{t+1}$ 的概率 $b_i(o_{t+1})$。

   这样还没结束，因为在 $t$ 时刻的状态 $i_t$ 有 $N$ 种，每种状态都有可能转移至 $t+1$ 时刻状态 $i_{t+1}$。因此我们要对 $t$ 时刻可能出现的所有状态 $i_t$ 进行累加。同时因为观测概率 $b_i(o_{o_{t+1}})$ 只与 $t+1$ 时刻的状态 $q_i$ 有关，与 $t$ 时刻的状态 $q_j$ 无关，因此可以将$b_i(o_{o_{t+1}})$ 提出至累加符号外。

3. 计算观测序列概率 $P(O\mid \lambda)$

   \[P(O|\lambda) = \sum_{i=1}^N \alpha_T(i) \tag{12}\]

   这个的思路和上面类似，把最终时刻 $T$ 的前向概率根据所有可能出现的状态 $q_i$ 全部累加起来，就可以得到截止至 $T$ 时刻产出观测序列 $O$ 的概率 $P(O\mid \lambda)$。

我们可以发现，采用前向概率计算 $P(O\mid \lambda)$ 的计算量是 $O(N^2 T)$。

后向概率

同样，给出后向概率的图解：

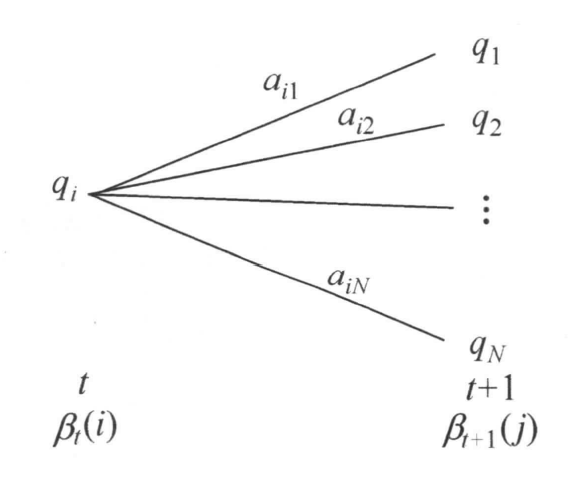
（来自《统计学习方法》201页）

后向概率：给定隐马尔可夫模型 $\lambda$，定义在时刻 $t$ 状态为 $q_i$ 的条件下，从 $t+1$ 到 $T$ 的部分观测序列为 $o_{t+1}, o_{t+2},…,o_T$ 的概率为后向概率 $\beta_t(i)$

\[\beta_t(i) = P(o_{t+1}, o_{t+2},...,o_T|i_t=q_i,\lambda) \tag{13}\]

同样地，我们可以采用递归的方法计算后向概率以及最终我们所需要的观测序列概率 $P(O\mid \lambda)$

1. 定义初始值 $\beta_T(i)$

   \[\beta_T(i) = 1,\qquad i=1,2,...,N \tag{14}\]

   大家可能会很好奇，为啥子这里 $\beta_T(i)=1$？莫慌，阿南给大家推导推导！

   首先我们可以把观测序列概率 $P(O\mid \lambda)$ 展开写成如下形式：

   \[\begin{aligned} P(O,i_t = q_i | \lambda) & = P(o_1,o_2,..,o_t,o_{t+1},...,o_T,i_t=q_i|\lambda) \\[2ex] & = P(o_1,o_2,..,o_t,i_t=q_i|\lambda) \times P(o_{t+1},...,o_T|i_t=q_i,\lambda) \\[2ex] & = \alpha_t(i) \times \beta_t(i) \end{aligned} \tag{15}\]

   然后我们令 $t=T$ 就会惊奇地发现

   \[\begin{aligned} P(O,i_t = q_i | \lambda) & = \alpha_T(i) \beta_T(i) \\ & = \alpha_T(i) \end{aligned} \tag{16}\]

   因此，在 $t=T$ 这种极端情况下，$\beta_T(i) = 1$

2. 对所有时刻 $t=T-1, T-2,…,1$：

   \[\beta_t(i) = \sum_{j=1}^N \beta_{t+1}(j) b_j(o_{t+1}) a_{ij}, \qquad i=1,2,...,N \tag{17}\]

   这个也很好理解。首先我们在已知 $t+1$ 时刻，即 $T$ 时刻时的后向概率 $\beta_T(i)$ 现在想要计算前一时刻 $t$ 的后向概率 $\beta_t(i)$——已知 $t$ 时刻状态为 $q_i$ 的情况下产生观测序列 $O(o_{t+1},…,o_T)$ 的概率。

   此时我们只需要将所有后一时刻 $t+1$ 关于状态 $q_j$ 的后向概率乘以在 $t+1$ 时刻可能产生观测 $o_{t+1}$ 的观测概率 $b_j(o_{t+1})$，再乘以状态转移概率 $a_{ij}$，然后把在 $t+1$ 时刻所有可能的状态 $q_j$ 累加起来即得 $t$ 时刻的后向概率 $\beta_t(i)$。

3. 最后计算观测序列概率 $P(O\mid \lambda)$

   \[P(O|\lambda) = \sum_{i=1}^N \pi_i b_i(o_1) \beta_1(i) \tag{18}\]

   这个地方也好理解，我用一个公式的推导来讲解吧！

   \[\begin{aligned} P(O,| \lambda) & = P(o_1,o_2,..,o_t,o_{t+1},...,o_T|\lambda) \\[2ex] & = \sum_{i=1}^N P(o_1|i_1=q_i, \lambda)P(o_2,..,o_t,o_{t+1},...,o_T|i_1 = q_i, \lambda) P(i_1=q_i) \\[2ex] & = \sum_{i=1}^N b_i(o_1) \beta_1(i) \pi_i \end{aligned} \tag{19}\]

   利用简单的条件概率公式就可以搞定啦！

OK！ 关于 前向概率 和 后向概率 的计算到这里相信大家都掌握了！接下来我们就用它们再去获得一些更有用的数据吧！

接下来我们用前向和后向概率去计算单个状态和两个状态概率的公式！

1. 给定模型 $\lambda$ 和观测 $O$，在时刻 $t$ 处于状态 $q_i$ 的概率。记为 $\gamma_t(i)$

   \[\gamma_t(i) = P(i_t=q_i|O,\lambda) \tag{20}\]

   为了用前向和后向概率进行表达，首先我们先分解上式

   \[\gamma_t(i) = P(i_t=q_i|O,\lambda) = \frac{P(i_t=q_i,O|\lambda)}{P(O|\lambda)} \tag{21}\]

   这时候我们惊喜的发现，上式的分子已经在式 $(15)$ 出现过了：

   \[P(O,i_t = q_i | \lambda) = \alpha_t(i) \beta_t(i) \tag{22}\]

   而对于分母的求解则可以直接通过上式对 $t$ 时刻所有状态的累加获得：

   \[P(O| \lambda) = \sum_{j=1}^N \alpha_t(j) \beta_t(j) \tag{23}\]

   于是得到：

   \[\gamma_t(i) = P(i_t=q_i|O,\lambda) = \frac{\alpha_t(i) \beta_t(i)}{\sum_{j=1}^N \alpha_t(j) \beta_t(j)} \tag{24}\]

2. 给定模型 $\lambda$ 和观测 $O$，在时刻 $t$ 处于状态 $q_i$ 且在时刻 $t+1$ 处于状态 $q_j$ 的概率。 记为 $\xi_t(i,j)$

   \[\xi_t(i,j) = P(i_t=q_i,i_{t+1}=q_j|O,\lambda) \tag{25}\]

   我们依旧可以将上式分解：

   \[\xi_t(i,j) = \frac{P(i_t = q_i,i_{t+1} = q_j,O|\lambda)}{P(O|\lambda)} = \frac{P(i_t = q_i,i_{t+1} = q_j,O|\lambda)}{\sum_{i=1}^N \sum_{j=1}^N P(i_t = q_i,i_{t+1} = q_j,O|\lambda)} \tag{26}\]

   其中我们在式 $(15)$ 的基础上继续进行如下推导：

   \[\begin{aligned} P(O,i_t = q_i, i_{t+1}=q_j | \lambda) & = P(o_1,o_2,..,o_t,o_{t+1},...,o_T,i_t=q_i|\lambda) \\[2ex] & = P(o_1,o_2,..,o_t,i_t=q_i|\lambda) \times P(o_{t+1},...,o_T|i_t=q_i,\lambda) \\[2ex] & = P(o_1,o_2,..,o_t,i_t=q_i|\lambda) \times P(i_{t+1}=q_j|i_t=q_i) \times P(o_{t+1}|i_{t+1}=q_j) \times P(o_{t+2},...,o_T|i_t=q_i,\lambda) \\[2ex] & = \alpha_t(i) \times a_{ij} \times b_j(o_{t+1}) \times \beta_{t+1}(i) \end{aligned} \tag{27}\]

   带回式 $(26)$ 即得：

   \[\xi_t(i,j) = \frac{\alpha_t(i) a_{ij} b_j(o_{t+1}) \beta_{t+1}(i)}{\sum_{i=1}^N \sum_{j=1}^N \alpha_t(i) a_{ij} b_j(o_{t+1}) \beta_{t+1}(i)} \tag{28}\]

• 在观测序列 $O$ 发生的情况下状态 $q_i$ 出现的期望值

  \[\sum_{t=1}^T \gamma_t(i) \tag{29}\]

  把所有时刻下可能会处于状态 $q_i$ 的概率全部累加起来即可

• 在观测 $O$ 下从状态 $q_i$ 转移至其它状态的期望值

  \[\sum_{t=1}^{T-1} \gamma_t(i) \tag{30}\]

  根据 组合 (Combination) 的思想，任意 $T-1$ 个时刻是 $q_i$ 状态，剩下的另一时刻是其它状态即满足要求。

• 在观测 $O$ 下从状态 $i$ 转移至状态 $j$ 的期望值

  \[\sum_{t=1}^{T-1} \xi_t(i,j) \tag{31}\]

  依旧是将 $T$ 时刻内所有可能从状态 $q_i$ 转移至 $q_j$ 的概率累加起来，一共有 $T-1$ 种情况。

好滴，关于隐马尔可夫的第一个基本问题——概率计算问题 到这里就结束啦！

接下来我们就进入第二个基本问题！

学习问题

隐马尔可夫模型的学习分为两种情况：

1. 不仅拥有观测序列 $O$，同时还掌握每个观测对应的状态序列 $I$。 那可真就太好办了，直接使用极大似然估计以频率表示概率来估计隐马尔可夫模型的参数。

首先讲第一种有状态序列的情况，这种也称为有监督学习，具体方法如下：

• 转移概率 $a_{ij}$ 的估计

  设样本中时刻 $t$ 处于状态 $i$ 并且于时刻 $t+1$ 转移到状态 $j$ 的频数为 $A_{ij}$，那么状态转移的概率 $a_{ij}$ 的估计是：

  \[\hat a_{ij} = \frac{A_{ij}}{\sum_{j=1}^N A_{ij}} \tag{32}\]

  即指定状态转变的频数 $A_{ij}$ 与 状态 $q_i$ 转移至所有可能的频数 $\sum_{j=1}^N A_{ij}$ 之比。

• 观测概率 $b_j(k)$ 的估计

  设样本中状态为 $j$ 并观测为 $k$ 的频数是 $B_{jk}$，那么状态为 $j$ 观测为 $k$ 的概率 $b_j(k)$ 的估计如下：

  \[b_j(k) = \frac{B_{jk}}{\sum_{k=1}^M B_{jk}} \tag{33}\]

  相似地，状态为 $j$ 并观测为 $k$ 的频数 $B_{jk}$ 除以状态为 $j$ 下所有可能出现的观测的频数之和 $\sum_{k=1}^M B_{jk}$ 即为结果。

• 初始状态概率 $\pi_i$ 的估计 $\hat \pi_i$ 为 $S$ 个样本中初始状态为 $q_i$ 的频率。

2. 仅拥有观测序列 $O$ 而不知对应的状态序列。 这个时候状态序列 $I$ 是隐藏起来不可观测的，那么我们应该如何学习隐马尔可夫模型 $\lambda=(A,B,\pi)$ 的参数呢？

这个时候机制的你会脱口而出：$EM$算法！ （详情参考 阿南带你理解EM算法）

没错！在这儿我们将观测序列数据视作观测数据 $O$，状态序列数据视作不可观测数据 $I$，那么隐马尔可夫模型实际上是包含有隐变量的概率模型：

\[P(O|\lambda) = \sum_I P(O|I,\lambda) P(I|\lambda) = \sum_I P(O,I|\lambda) \tag{34}\]

上式的参数学习可以由 $EM$算法 实现，通常在隐马尔可夫模型中也称为 $Baum-Welch$ 算法。

Baum-Welch 算法

1. 确定完全数据的对数似然函数 所有观测数据为 $O=(o_1,o_2,…,o_T)$，所有隐数据写成 $I=(i_1,i_2,…,i_T)$。因此，完全数据写成 $(O,I)=(o_1,o_2,…,o_T,i_1,i_2,…,i_T)$。

   完全数据的对数似然函数是：$\log P(O,I\mid \lambda)$

2. $EM$算法的 $E$ 步：定义 $Q$函数 $Q(\lambda,\bar \lambda)$

   与 $EM$算法 一致，此处的 $Q$函数 为完全数据的对数似然函数 $\log P(O,I\mid \lambda)$ 关于隐变量 $I$ 的条件期望：

   \[\begin{aligned} Q(\lambda,\bar \lambda) & = \sum_I P(I|O,\bar \lambda) \log P(O,I|\lambda) \\[2ex] & = \sum_I \frac{P(I,O|\bar \lambda)}{P(O|\bar \lambda)} \log P(O,I|\lambda) \\[2ex] & \propto \sum_I P(I,O|\bar \lambda) \log P(O,I|\lambda) \end{aligned} \tag{35}\]

   可以发现上式第二步略去了与隐藏序列 $I$ 无关的 $\frac{1}{P(O\mid \bar \lambda)}$，因为其只是一个常数，并不影响后续 $Q$函数关于参数的优化问题。

   式 $(35)$ 中 $\bar \lambda$ 是隐马尔可夫模型参数的当前估计值，如果是第一轮则需要我们人为地初始化。至于 $\lambda$ 则是我们需要极大化的隐马尔可夫模型参数。并且我们可以将完全数据的联合概率 $P(O,I\mid \lambda)$ 做如下分解：

   \[\begin{aligned} P(O,I|\lambda) & = P(I|\lambda) P(O|I,\lambda) \\[2ex] & = \pi_{i1}a_{i_1i_2}\cdots a_{i_{T-1}i_T} \times b_{i_1}(o_1) b_{i_2}(o_2)\cdots b_{i_{T}}(o_T) \\[2ex] & = \pi_{i1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)\cdots a_{i_{T-1}i_T}b_{i_{T}}(o_T) \end{aligned} \tag{36}\]

   因此只需简单地把式 $(36)$ 中的乘法变成了对数的加法，便可将 $Q$函数改写为：

   \[Q(\lambda,\bar \lambda) = \sum_I \log \pi_{i_1} P(O,I|\bar \lambda) + \sum_I \left(\sum_{t=1}^{T-1} \log a_{i_t i_{t-1}} \right) P(O,I|\bar \lambda) + \sum_I \left(\sum_{t=1}^{T} \log b_{i_t}(o_t) \right) P(O,I|\bar \lambda) \tag{37}\]

3. $EM$算法的 $M$ 步：极大化 $Q$函数 $Q(\lambda,\bar \lambda)$，求解模型参数 $A,B,\pi$

   由于我们要极大化的参数分别出现在式 $(37)$ 的三个项中，因此我们只需要对这三个项分别进行极大化即可。

   • 计算初始概率分布 $\pi_i$

     式 $(37)$ 的第一项可以写做为：

     \[\begin{aligned} \sum_I \log \pi_i P(O,I|\bar \lambda) & = \sum_{i_1} \sum_{i_2} \cdots \sum_{i_T} \log \pi_i P(O,i_1,i_2,...,i_T |\bar \lambda) \\[2ex] & = \sum_{i=1}^N \log \pi_i P(O,i_1=i |\bar \lambda) \\[2ex] & s.t. \sum_{i=1}^N \pi_i = 1 \end{aligned} \\ \tag{38}\]

     式 $(38)$ 是一个有约束问题，我们利用 拉格朗日乘子法 将其构建成为一个无约束问题：

     \[L(\alpha,\pi) = \sum_{i=1}^N \log \pi P(O,i_1=i|\bar \lambda) + \alpha (\sum_{i=1}^N \pi_i -1 ) \tag{39}\]

     对其求偏导并令其结果为零，解出拉格朗日乘子 $\alpha$:

     \[\frac{\partial}{\partial \pi_i} \left[\sum_{i=1}^N \log \pi P(O,i_1=i|\bar \lambda) + \alpha (\sum_{i=1}^N \pi_i -1) \right] = 0 \tag{40}\]

     得： \(P(O,i_1=1|\bar \lambda) + \alpha \pi_i = 0 \tag{41}\)

     此处利用 $\sum_{i=1}^N \pi_i = 1$ 的性质，我们对上式 $(41)$ 求关于 $i$ 的累加和：

     \[\sum_{i=1}^N P(O,i_1=1|\bar \lambda) + \alpha \pi_i \Longleftrightarrow P(O|\bar \lambda) + \alpha \tag{42}\]

     因此解得拉格朗日乘子 $\alpha$:

     \[\alpha = -P(O|\bar \lambda)\]

     将其代回至式 $(41)$ 解得 初始概率分布新一轮的估计值 $\hat \pi_i$：

     \[\hat \pi_i = \frac{\sum_{i=1}^N P(O,i_1=1|\bar \lambda)}{P(O|\bar \lambda)} \tag{43}\]

   • 计算转移概率 $a_{ij}$

     同理，式 $(37)$ 的第二项可以改写为：

     \[\begin{aligned} \sum_I \left(\sum_{t=1}^{T-1} \log a_{i_t i_{t-1}} \right) P(O,I|\bar \lambda) & = \sum_{i=1}^N \sum_{j=1}^N \sum_{t=1}^{T-1} \log a_{i_t i_{t-1}} P(O,i_t = i,i_{t+1}=j|\bar \lambda) \\ & s.t. \sum_{i=1}^N \pi_i = 1 \end{aligned} \tag{44}\]

     类似地，对式 $(44)$ 构建拉格朗日方程求解出 转移概率新一轮的估计值 $\hat a_{ij}$：

     \[\hat a_{ij} = \frac{\sum_{t=1}^{T-1}P(O,i_t=i,i_{t+1}=j|\bar \lambda)}{\sum_{t=1}^{T-1}P(O,i_t=i|\bar \lambda)} \tag{45}\]

   • 计算观测概率 $b_j{(k)}$

     同理，改写式 $(37)$ 的第三项为：

     \[\sum_I \left(\sum_{t=1}^{T} \log b_{i_t}(o_t) \right) P(O,I|\bar \lambda) = \sum_{j=1}^N \sum_{t=1}^{T} \log b_{j}(o_t) P(O,i_t=j|\bar \lambda) \tag{46}\]

     相似地，约束条件是 $\sum_{j=1}^N b_j(k) = 1$，利用拉格朗日乘子法可以求得 观测概率新一轮的估计值 $\hat b_{j}(k)$：

     \[\hat b_j(k) = \frac{\sum_{t=1}^T P(O,i_t=j|\bar \lambda) I (o_t=v_k)}{P(O,i_t=j|\bar \lambda)} \tag{47}\]

     为了简单表示，我们可以用之前提到过的 单个状态概率 $\gamma_t(i)$ 和 两个状态概率 $\xi_t (i,j)$ 去表示上面的三个公式：

     \[\begin{aligned} \hat \pi_i & = \frac{\sum_{i=1}^N P(O,i_1=1|\bar \lambda)}{P(O|\bar \lambda)} = \frac{\sum_{t=1}^{T-1} \xi_t(i,j)}{\sum_{t=1}^{T-1}\gamma_t(i)} \\[2ex] \hat a_{ij} & = \frac{\sum_{t=1}^{T-1}P(O,i_t=i,i_{t+1}=j|\bar \lambda)}{\sum_{t=1}^{T-1}P(O,i_t=i|\bar \lambda)} = \frac{\sum_{t=1}^{T-1} \xi_t(1,j)}{\sum_{t=1}^{T-1} \gamma_t(i)} \\[2ex] \hat b_j(k) & = \frac{\sum_{t=1}^T P(O,i_t=j|\bar \lambda) I (o_t=v_k)}{P(O,i_t=j|\bar \lambda)} = \frac{\sum_{t=1,o_t=v_k}^T \gamma_t(j)}{\sum_{t=1}^T \gamma_t(j)} \\[2ex] \end{aligned} \tag{48}\]

好滴，关于预测算法就介绍到这里啦~

接下来就是我们的最后一个基本问题：预测算法！

预测问题

怕大家看了前两个长长的基本问题之后就忘记预测问题是啥子了，于是阿南在这里再带大家回顾一下！

预测问题： 在已知模型 $\lambda = (A,B,\pi)$ 和观测序列 $O=(o_1, o_2,…,o_T)$, 求对给定观测序列 $O$ 下最有可能的状态序列 $I=(i_1, i_2,…,i_T)$。即给定观测序列，求最有可能对应的状态序列。

这里我们可以采用两种方法去计算，分别是 近似算法 和 维特比算法。接下来我将分别介绍这两种算法。

近似算法

近似算法的核心思想就是，在每个时刻 $t$ 选择出当前时刻最有可能出现的状态 $i_t^{*}$，从而得到一个状态序列 $I^{*} = (i_1^{*},i_2^{*},…,i_T^{*})$，将其作为最有可能出现的序列的预测结果。

回想我们之前对于 $\gamma_t(i)$ 的定义，即 $t$ 时刻状态为 $q_i$ 的概率：

\[\gamma_t(i) = P(i_t=q_i|O,\lambda) = \frac{P(i_t=q_i,O|\lambda)}{P(O|\lambda)} \tag{49}\]

在每一时刻 $t$ 最有可能的状态 $i_t^{*}$ 我们就可以本能地认为是 $\gamma_t(i)$ 最大时所对应的状态 $q_i$:

\[i_t^{*} = \arg \max_{1\le i \le N} [\gamma_t(i)],\qquad t=1,2,...,T \tag{50}\]

按照上述方法遍历计算所有的时刻，从而得到 “最有可能的状态序列” $I^{*} = (i_1^{*},i_2^{*},…,i_T^{*})$

这里为什么把最有可能打上引号呢？原因就是尽管按照上述方法计算比较简单，但是存在一个致命的缺点其只能保证计算出来的每个 $i_t^{*}$ 是当前某一个 $t$ 时刻最有可能的单个状态，而不能保证预测的状态序列整体是最有可能的状态序列。***因为预测的状态序列可能有实际不发生的部分，即可能存在某两个相邻状态之间的转移概率 $a_{ij}=0$ 的情况发生。

当然啦！尽管有这样的缺陷，但是 近似算法 在某些情况下仍然是适用滴！

接下来要讲的就是在面试中频频出现的 维特比算法！

维特比算法

维特比算法实际上是运用了 动态规划 的思想来解概率最大路径（最优路径）。

根据动态规划的原理，最优路径具有如下特性：如果最优路径在时刻 $t$ 通过节点 $i_t^{*}$，那么这一路径从节点 $i_t^{*}$ 到终点 $i_T^{*}$ 的部分路径，对于从 $i_t^{*}$ 到 $i_T^{*}$ 的所有可能的路径来说都必须是最优的。

根据这一原理，我们只需从时刻 $t=1$ 开始，递推地计算在时刻 $t$ 状态为 $i$ 的各条部分路径的最大概率，直到得到最终时刻 $t=T$ 状态为 $i$ 的各条路径的最大概率。

时刻 $t=T$ 的最大概率即为最优路径的概率 $P^{*}$，同时也得到最优终结点 $i_T^{*}$。此时再将综合之前所记录的最优节点 $i_t^{*}, \qquad t=1,2,…,T-1$ 即可得到最优路径 $I^{*} = (i_1^{*}, i_2^{*},…,i_T^{*})$。这就是维特比算法。

此处我们首先定义两个变量 $\delta$ 和 $\Psi$。

定义：在时刻 $t$ 状态为 $i$ 的所有单个路径 $(i_1, i_2,…,i_t)$ 中概率最大值为：

\[\delta_t(i) = \max_{i_{1},i_{2},...,i_{t-1}} P(i_t = i,i_{t-1},...,i_1,o_t,...,o_1|\lambda),\qquad i=1,2,...,N \tag{51}\]

根据定义我们可以递归地求出变量 $\delta$ 的递推公式：

\[\delta_{t+1}(j) = \max_{1\le j\le N} [\delta_t(i) a_{ij}] b_j(o_{t+1}) \tag{52}\]

同时定义在时刻 $t$ 状态为 $i$ 的所有单个路径 $(i_1,i_2,…,i_{t-1}, i_t = q_i)$ 中概率最大的路径在 $t-1$ 时刻的结点为： \(\Psi_t(i) = \arg \max_{1\le j\le N} [\delta_{t-1}(j)a_{ij}], \qquad i=1,2,...,N \tag{53}\)

准备工作已经做好了，现在让我们正式开始 维特比算法 吧！

输入： 模型 $\lambda = (A,B,\pi)$ 和 观测 $O=(o_1,o_2,…,o_T)$

输出： 最优路径 $I^{*} = (i_1^{*}, i_2^{*},…,i_T^{*})$

1. 计算初始值

   \[\begin{aligned} \delta_1(i) & = \pi_i b_i(o_1),& \qquad i & = 1,2,...,N \\[2ex] \Psi_1(i) & = 0,& i & = 1,2,...,N \end{aligned} \tag{54}\]

2. 递归地计算所有时刻的值,对 $t=1,2,…,T-1$

   \[\begin{aligned} \delta_{t+1}(j) &= \max_{1\le j\le N} [\delta_t(i) a_{ij}] b_j(o_{t+1}),& \qquad i & = 1,2,...,N \\[2ex] \Psi_{t+1}(i) &= \arg \max_{1\le j\le N} [\delta_{t}(j)a_{ij}],& i & = 1,2,...,N \end{aligned} \tag{55}\]

   按照上述公式遍历计算当前时刻 $t+1$ 的每个状态 $i_{t+1} = q_j, j=1,2,…,N$ 得到每个对应的 $\delta_{t+1}(j)$，分别表示当前 $t+1$ 时刻的每个状态 $q_j$ 结合从初始时刻 $t=1$ 至时刻 $t=t$ 时已经得到对于当前时刻 $t+1$ 的最可能的状态序列 $I_{t}^{*}$，得到的 $I_{t+1}^{*} = (i_1^{*}, i_2^{*},…,i_t^{*},i_{t+1}^{*}=q_j),\ j=1,2,…,N$ 产生观测序列 $O_{t+1}=(o_1,…,o_{t+1})$ 的概率值。

   而 $\Psi_{t+1}(i)$ 则记录了当前 $t+1$ 时刻的状态 $i_{t+1} = q_j, j=1,2,…,N$ 所链接的上一个时刻的状态 $i_t$。

3. 计算至终点 $T$ 时刻时停止计算

   \[\begin{aligned} P^{*} & = \max_{1\le i\le N} \delta_T(i) \\[2ex] i_T^{*} & = \arg \max_{1\le i \le N} [\delta_T(i)] \end{aligned} \tag{56}\]

4. 确定终点的状态 $i_T=q_i$ 之后就可以 $\Psi_{T}(i)$ 找到前一时刻 $T-1$ 的最优状态 $i_{T-1}=q_j$，依此类推我们就可以从终点一直回溯至起点时刻，找到最优路径 $I^{*} = (i_1^{*}, i_2^{*},…,i_T^{*})$

铛铛！关于隐马尔可夫模型的最后一个 预测问题 也讲完啦！希望大家到这里都能对 隐马尔科夫模型 有一种框架感！

总结

说一说 HMM、CRF、RNN 这三个模型之间最本质的联系和区别吧！

联系： 这三者都可以看成图。

区别：

• HMM 属于有向图，且有两个非常强的假设，即当前状态只与前一状态有关还有观察值之间的严格独立。

  同时 HMM 是生成模型，而 Linear-CRF 是判别模型。

• CRF 属于无向图，是一个有条件的马尔可夫随机场。

• RNN 算是有向图，深度学习讲究的是最小化先验表征和计算假设，避免明确的手工设计结构。

---

• Previous
  阿南带你理解 AdaBoost
• Next
  阿南带你理解梯度提升树